Expectation–maximization algorithm
In statistics, an expectation–maximization (EM) algorithm is an iterative method for finding maximum likelihood or maximum a posteriori (MAP) estimates of parameters in statistical models, where the model depends on unobserved latent variables. The EM iteration alternates between performing an expectation (E) step, which computes the expectation of the log-likelihood evaluated using the current estimate for the parameters, and a maximization (M) step, which computes parameters maximizing the expected log-likelihood found on the E step. These parameter-estimates are then used to determine the distribution of the latent variables in the next E step.
Contents |
History
The EM algorithm was explained and given its name in a classic 1977 paper by Arthur Dempster, Nan Laird, and Donald Rubin.[1] They pointed out that the method had been "proposed many times in special circumstances" by earlier authors. In particular, a very detailed treatment of the EM method for exponential families was published by Rolf Sundberg in his thesis and several papers[2][3][4] following his collaboration with Per Martin-Löf and Anders Martin-Löf.[5][6][7][8][9][10][11] The Dempster-Laird-Rubin paper in 1977 generalized the method and sketched a convergence analysis for a wider class of problems. Regardless of earlier inventions, the innovative Dempster-Laird-Rubin paper in the Journal of the Royal Statistical Society received an enthusiastic discussion at the Royal Statistical Society meeting with Sundberg calling the paper "brilliant". The Dempster-Laird-Rubin paper established the EM method as an important tool of statistical analysis.
The convergence analysis of the Dempster-Laird-Rubin paper was flawed and a correct convergence analysis was published by C. F. Jeff Wu in 1983. Wu's proof established the EM method's convergence outside of the exponential family, as claimed by Dempster-Laird-Rubin.[12]
Description
Given a statistical model consisting of a set 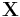 of observed data, a set of unobserved latent data or missing values
of observed data, a set of unobserved latent data or missing values 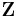 , and a vector of unknown parameters
, and a vector of unknown parameters 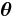 , along with a likelihood function
, along with a likelihood function  , the maximum likelihood estimate (MLE) of the unknown parameters is determined by the marginal likelihood of the observed data
, the maximum likelihood estimate (MLE) of the unknown parameters is determined by the marginal likelihood of the observed data
However, this quantity is often intractable.
The EM algorithm seeks to find the MLE of the marginal likelihood by iteratively applying the following two steps:
- Expectation step (E step): Calculate the expected value of the log likelihood function, with respect to the conditional distribution of
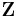 given
given 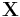 under the current estimate of the parameters
under the current estimate of the parameters 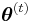 :
:
- Maximization step (M step): Find the parameter that maximizes this quantity:
Note that in typical models to which EM is applied:
- The observed data points
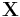 may be discrete (taking values in a finite or countably infinite set) or continuous (taking values in an uncountably infinite set). There may in fact be a vector of observations associated with each data point.
may be discrete (taking values in a finite or countably infinite set) or continuous (taking values in an uncountably infinite set). There may in fact be a vector of observations associated with each data point. - The missing values (aka latent variables)
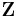 are discrete, drawn from a fixed number of values, and there is one latent variable per observed data point.
are discrete, drawn from a fixed number of values, and there is one latent variable per observed data point. - The parameters are continuous, and are of two kinds: Parameters that are associated with all data points, and parameters associated with a particular value of a latent variable (i.e. associated with all data points whose corresponding latent variable has a particular value).
However, it is possible to apply EM to other sorts of models.
The motivation is as follows. If we know the value of the parameters 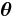 , we can usually find the value of the latent variables
, we can usually find the value of the latent variables 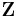 by maximizing the log-likelihood over all possible values of
by maximizing the log-likelihood over all possible values of 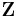 , either simply by iterating over
, either simply by iterating over 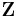 or through an algorithm such as the Viterbi algorithm for hidden Markov models. Conversely, if we know the value of the latent variables
or through an algorithm such as the Viterbi algorithm for hidden Markov models. Conversely, if we know the value of the latent variables 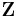 , we can find an estimate of the parameters
, we can find an estimate of the parameters 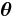 fairly easily, typically by simply grouping the observed data points according to the value of the associated latent variable and averaging the values, or some function of the values, of the points in each group. This suggests an iterative algorithm, in the case where both
fairly easily, typically by simply grouping the observed data points according to the value of the associated latent variable and averaging the values, or some function of the values, of the points in each group. This suggests an iterative algorithm, in the case where both 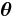 and
and 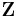 are unknown:
are unknown:
- First, initialize the parameters
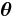 to some random values.
to some random values. - Compute the best value for
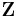 given these parameter values.
given these parameter values. - Then, use the just-computed values of
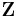 to compute a better estimate for the parameters
to compute a better estimate for the parameters 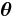 . Parameters associated with a particular value of
. Parameters associated with a particular value of 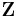 will use only those data points whose associated latent variable has that value.
will use only those data points whose associated latent variable has that value. - Iterate steps 2 and 3 until convergence.
The algorithm as just described monotonically approaches a local minimum of the cost function, and is commonly called hard EM. The k-means algorithm is an example of this class of algorithms.
However, we can do somewhat better by, rather than making a hard choice for 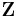 given the current parameter values and averaging only over the set of data points associated with a particular value of
given the current parameter values and averaging only over the set of data points associated with a particular value of 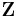 , instead determining the probability of each possible value of
, instead determining the probability of each possible value of 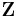 for each data point, and then using the probabilities associated with a particular value of
for each data point, and then using the probabilities associated with a particular value of 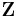 to compute a weighted average over the entire set of data points. The resulting algorithm is commonly called soft EM, and is the type of algorithm normally associated with EM. The counts used to compute these weighted averages are called soft counts (as opposed to the hard counts used in a hard-EM-type algorithm such as k-means). The probabilities computed for
to compute a weighted average over the entire set of data points. The resulting algorithm is commonly called soft EM, and is the type of algorithm normally associated with EM. The counts used to compute these weighted averages are called soft counts (as opposed to the hard counts used in a hard-EM-type algorithm such as k-means). The probabilities computed for 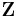 are posterior probabilities and are what is computed in the E step. The soft counts used to compute new parameter values are what is computed in the M step.
are posterior probabilities and are what is computed in the E step. The soft counts used to compute new parameter values are what is computed in the M step.
Properties
Speaking of an expectation (E) step is a bit of a misnomer. What is calculated in the first step are the fixed, data-dependent parameters of the function Q. Once the parameters of Q are known, it is fully determined and is maximized in the second (M) step of an EM algorithm.
Although an EM iteration does increase the observed data (i.e. marginal) likelihood function there is no guarantee that the sequence converges to a maximum likelihood estimator. For multimodal distributions, this means that an EM algorithm may converge to a local maximum of the observed data likelihood function, depending on starting values. There are a variety of heuristic or metaheuristic approaches for escaping a local maximum such as random restart (starting with several different random initial estimates θ(t)), or applying simulated annealing methods.
EM is particularly useful when the likelihood is an exponential family: the E step becomes the sum of expectations of sufficient statistics, and the M step involves maximizing a linear function. In such a case, it is usually possible to derive closed form updates for each step, using the Sundberg formula (published by Rolf Sundberg using unpublished results of Per Martin-Löf and Anders Martin-Löf).[3][4][7][8][9][10][11]
The EM method was modified to compute maximum a posteriori (MAP) estimates for Bayesian inference in the original paper by Dempster, Laird, and Rubin.
There are other methods for finding maximum likelihood estimates, such as gradient descent, conjugate gradient or variations of the Gauss–Newton method. Unlike EM, such methods typically require the evaluation of first and/or second derivatives of the likelihood function.
Alternative description
Under some circumstances, it is convenient to view the EM algorithm as two alternating maximization steps.[13][14] Consider the function:
where q is an arbitrary probability distribution over the unobserved data z, pZ|X(· |x;θ) is the conditional distribution of the unobserved data given the observed data x, H is the entropy and DKL is the Kullback–Leibler divergence.
Then the steps in the EM algorithm may be viewed as:
- Expectation step: Choose q to maximize F:
- Failed to parse (PNG conversion failed;
check for correct installation of latex, dvips, gs, and convert): q^{(t)} = \operatorname*{arg\,max}_q \ F(q,\theta^{(t)})
- Maximization step: Choose θ to maximize F:
- Failed to parse (PNG conversion failed;
check for correct installation of latex, dvips, gs, and convert): \theta^{(t+1)} = \operatorname*{arg\,max}_\theta \ F(q^{(t)},\theta)
Applications
EM is frequently used for data clustering in machine learning and computer vision. In natural language processing, two prominent instances of the algorithm are the Baum-Welch algorithm (also known as forward-backward) and the inside-outside algorithm for unsupervised induction of probabilistic context-free grammars.
In psychometrics, EM is almost indispensable for estimating item parameters and latent abilities of item response theory models.
With the ability to deal with missing data and observe unidentified variables, EM is becoming a useful tool to price and manage risk of a portfolio.
The EM algorithm (and its faster variant Ordered subset expectation maximization) is also widely used in medical image reconstruction, especially in positron emission tomography and single photon emission computed tomography. See below for other faster variants of EM.
Variants
A number of methods have been proposed to accelerate the sometimes slow convergence of the EM algorithm, such as those utilising conjugate gradient and modified Newton–Raphson techniques.[15] Additionally EM can be utilised with constrained estimation techniques.
Expectation conditional maximization (ECM) replaces each M step with a sequence of conditional maximization (CM) steps in which each parameter θi is maximized individually, conditionally on the other parameters remaining fixed.[16]
This idea is further extended in generalized expectation maximization (GEM) algorithm, in which one only seeks an increase in the objective function F for both the E step and M step under the alternative description.[13]
It is also possible to consider the EM algorithm as a subclass of the MM (Majorize/Minimize or Minorize/Maximize, depending on context) algorithm,[17] and therefore use any machinery developed in the more general case.
Relation to variational Bayes methods
EM is a partially non-Bayesian, maximum likelihood method. Its final result gives a probability distribution over the latent variables (in the Bayesian style) together with a point estimate for θ (either a maximum likelihood estimate or a posterior mode). We may want a fully Bayesian version of this, giving a probability distribution over θ as well as the latent variables. In fact the Bayesian approach to inference is simply to treat θ as another latent variable. In this paradigm, the distinction between the E and M steps disappears. If we use the factorized Q approximation as described above (variational Bayes), we may iterate over each latent variable (now including θ) and optimize them one at a time. There are now k steps per iteration, where k is the number of latent variables. For graphical models this is easy to do as each variable's new Q depends only on its Markov blanket, so local message passing can be used for efficient inference.
Geometric interpretation
In information geometry, the E step and the M step are interpreted as projections under dual affine connections, called the e-connection and the m-connection; the Kullback–Leibler divergence can also be understood in these terms.
Example: Gaussian mixture
Let x = (x1,x2,…,xn) be a sample of n independent observations from a mixture of two multivariate normal distributions of dimension d, and let z=(z1,z2,…,zn) be the latent variables that determine the component from which the observation originates.[14]
 and
and 
where
 and
and 
The aim is to estimate the unknown parameters representing the "mixing" value between the Gaussians and the means and covariances of each:
where the likelihood function is:
where 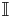 is an indicator function and f is the probability density function of a multivariate normal. This may be rewritten in exponential family form:
is an indicator function and f is the probability density function of a multivariate normal. This may be rewritten in exponential family form:
E step
Given our current estimate of the parameters θ(t), the conditional distribution of the Zi is determined by Bayes theorem to be the proportional height of the normal density weighted by τ:
 .
.
Thus, the E step results in the function:
M step
The quadratic form of Q(θ|θ(t)) means that determining the maximising values of θ is relatively straightforward. Firstly note that τ, (μ1,Σ1) and (μ2,Σ2) may be all maximised independently of each other since they all appear in separate linear terms.
Firstly, consider τ, which has the constraint τ1 + τ2=1:
This has the same form as the MLE for the binomial distribution, so:
For the next estimates of (μ1,Σ1):
This has the same form as a weighted MLE for a normal distribution, so
 and
and 
and, by symmetry:
 and
and  .
.
References
- Robert Hogg, Joseph McKean and Allen Craig. Introduction to Mathematical Statistics. pp. 359–364. Upper Saddle River, NJ: Pearson Prentice Hall, 2005.
- The on-line textbook: Information Theory, Inference, and Learning Algorithms, by David J.C. MacKay includes simple examples of the EM algorithm such as clustering using the soft k-means algorithm, and emphasizes the variational view of the EM algorithm.
- Theory and Use of the EM Method by M. R. Gupta and Y. Chen is a well-written short book on EM, including detailed derivation of EM for GMMs, HMMs, and Dirichlet.
- A Gentle Tutorial of the EM Algorithm and its Application to Parameter Estimation for Gaussian Mixture and Hidden Markov Models, by Jeff Bilmes includes a simplified derivation of the EM equations for Gaussian Mixtures and Gaussian Mixture Hidden Markov Models.
- Variational Algorithms for Approximate Bayesian Inference, by M. J. Beal includes comparisons of EM to Variational Bayesian EM and derivations of several models including Variational Bayesian HMMs (chapters).
- The Expectation Maximization Algorithm, by Frank Dellaert, gives an easier explanation of EM algorithm in terms of lowerbound maximization.
- The Expectation Maximization Algorithm: A short tutorial, A self contained derivation of the EM Algorithm by Sean Borman.
- The EM Algorithm, by Xiaojin Zhu.
- EM algorithm and variants: an informal tutorial by Alexis Roche. A concise and very clear description of EM and many interesting variants.
- Bishop, Christopher M. (2006). Pattern Recognition and Machine Learning. Springer. ISBN 0-387-31073-8.
References
- ^ Dempster, A.P.; Laird, N.M.; Rubin, D.B. (1977). "Maximum Likelihood from Incomplete Data via the EM Algorithm". Journal of the Royal Statistical Society. Series B (Methodological) 39 (1): 1–38. JSTOR 2984875. MR0501537.
- ^ Sundberg, Rolf (1974). "Maximum likelihood theory for incomplete data from an exponential family". Scandinavian Journal of Statistics 1 (2): 49–58. JSTOR 4615553. MR381110.
- ^ a b Rolf Sundberg. 1971. Maximum likelihood theory and applications for distributions generated when observing a function of an exponential family variable. Dissertation, Institute for Mathematical Statistics, Stockholm University.
- ^ a b Sundberg, Rolf (1976). "An iterative method for solution of the likelihood equations for incomplete data from exponential families". Communications in Statistics – Simulation and Computation 5 (1): 55–64. doi:10.1080/03610917608812007. MR443190.
- ^ See the acknowledgement by Dempster, Laird and Rubin on pages 3, 5 and 11.
- ^ G. Kulldorff. 1961. Contributions to the theory of estimation from grouped and partially grouped samples. Almqvist & Wiksell.
- ^ a b Anders Martin-Löf. 1963. "Utvärdering av livslängder i subnanosekundsområdet" ("Evaluation of sub-nanosecond lifetimes"). ("Sundberg formula")
- ^ a b Per Martin-Löf. 1966. Statistics from the point of view of statistical mechanics. Lecture notes, Mathematical Institute, Aarhus University. ("Sundberg formula" credited to Anders Martin-Löf).
- ^ a b Per Martin-Löf. 1970. Statistika Modeller (Statistical Models): Anteckningar från seminarier läsåret 1969–1970 (Notes from seminars in the academic year 1969-1970), with the assistance of Rolf Sundberg. Stockholm University. ("Sundberg formula")
- ^ a b Martin-Löf, P. The notion of redundancy and its use as a quantitative measure of the deviation between a statistical hypothesis and a set of observational data. With a discussion by F. Abildgård, A. P. Dempster, D. Basu, D. R. Cox, A. W. F. Edwards, D. A. Sprott, G. A. Barnard, O. Barndorff-Nielsen, J. D. Kalbfleisch and G. Rasch and a reply by the author. Proceedings of Conference on Foundational Questions in Statistical Inference (Aarhus, 1973), pp. 1–42. Memoirs, No. 1, Dept. Theoret. Statist., Inst. Math., Univ. Aarhus, Aarhus, 1974.
- ^ a b Martin-Löf, Per The notion of redundancy and its use as a quantitative measure of the discrepancy between a statistical hypothesis and a set of observational data. Scand. J. Statist. 1 (1974), no. 1, 3–18.
- ^ Wu, C. F. Jeff (Mar. 1983). "On the Convergence Properties of the EM Algorithm". Annals of Statistics 11 (1): 95–103. doi:10.1214/aos/1176346060. JSTOR 2240463. MR684867.
- ^ a b Neal, Radford; Hinton, Geoffrey (1999). Michael I. Jordan. ed. "A view of the EM algorithm that justifies incremental, sparse, and other variants". Learning in Graphical Models (Cambridge, MA: MIT Press): 355–368. ISBN 0262600323. ftp://ftp.cs.toronto.edu/pub/radford/emk.pdf. Retrieved 2009-03-22.
- ^ a b Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome (2001). "8.5 The EM algorithm". The Elements of Statistical Learning. New York: Springer. pp. 236–243. ISBN 0-387-95284-5.
- ^ Jamshidian, Mortaza; Jennrich, Robert I. (1997). "Acceleration of the EM Algorithm by using Quasi-Newton Methods". Journal of the Royal Statistical Society: Series B (Statistical Methodology) 59 (2): 569–587. doi:10.1111/1467-9868.00083. MR1452026.
- ^ Meng, Xiao-Li; Rubin, Donald B. (1993). "Maximum likelihood estimation via the ECM algorithm: A general framework". Biometrika 80 (2): 267–278. doi:10.1093/biomet/80.2.267. MR1243503.
- ^ Hunter DR and Lange K (2004), A Tutorial on MM Algorithms, The American Statistician, 58: 30-37
External links
- Various 1D, 2D and 3D demonstrations of EM together with Mixture Modeling are provided as part of the paired SOCR activities and applets. These applets and activities show empirically the properties of the EM algorithm for parameter estimation in diverse settings.
- Class hierarchy in C++ (GPL) including Gaussian Mixtures

![Q(\boldsymbol\theta|\boldsymbol\theta^{(t)}) = \operatorname{E}_{\mathbf{Z}|\mathbf{X},\boldsymbol\theta^{(t)}}\left[ \log L (\boldsymbol\theta;\mathbf{X},\mathbf{Z}) \right] \,](/2012-wikipedia_en_all_nopic_01_2012/I/55b619a3c1c7e7dee6d9d2909925525f.png)

![F(q,\theta) = \operatorname{E}_q [ \log L (\theta�; x,Z) ] %2B H(q) = -D_{\mathrm{KL}}\big(q \big\| p_{Z|X}(\cdot|x;\theta ) \big) %2B \log L(\theta;x)](/2012-wikipedia_en_all_nopic_01_2012/I/bcbf40525399e1008635c937e9c46bfc.png)


![L(\theta;\mathbf{x},\mathbf{z}) = \exp \left\{ \sum_{i=1}^n \sum_{j=1}^2 \mathbb{I}(z_i=j) \big[ \log \tau_j -\tfrac{1}{2} \log |\Sigma_j| -\tfrac{1}{2}(\mathbf{x}_i-\boldsymbol{\mu}_j)^\top\Sigma_j^{-1} (\mathbf{x}_i-\boldsymbol{\mu}_j) -\tfrac{d}{2} \log(2\pi) \big] \right\}](/2012-wikipedia_en_all_nopic_01_2012/I/d53e50b61c8d3465b6bd20e085933f6a.png)
![\begin{align}Q(\theta|\theta^{(t)})
&= \operatorname{E} [\log L(\theta;\mathbf{x},\mathbf{Z}) ] \\
&= \sum_{i=1}^n \sum_{j=1}^2 T_{j,i}^{(t)} \big[ \log \tau_j -\tfrac{1}{2} \log |\Sigma_j| -\tfrac{1}{2}(\mathbf{x}_i-\boldsymbol{\mu}_j)^\top\Sigma_j^{-1} (\mathbf{x}_i-\boldsymbol{\mu}_j) -\tfrac{d}{2} \log(2\pi) \big]
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/84efae4d173871c8ffb2f53a0c67595f.png)
![\begin{align}\boldsymbol{\tau}^{(t%2B1)}
&= \underset{\boldsymbol{\tau}} {\operatorname{arg\,max}}\ Q(\theta | \theta^{(t)} ) \\
&= \underset{\boldsymbol{\tau}} {\operatorname{arg\,max}} \ \left\{ \left[ \sum_{i=1}^n T_{1,i}^{(t)} \right] \log \tau_1 %2B \left[ \sum_{i=1}^n T_{2,i}^{(t)} \right] \log \tau_2 \right\}
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/8722febd91bcb471081c99602a3445a4.png)

